ブラックホールのシンギュラリティは、期待どおりに避けられない

(図 Fractal Pixabay by chiplanay)　　(Fig.) アーティクル・イメージ

初めて、物理学者達は、現実的なブラックホールの中心にどのような種類の特異点があるかを正確に計算しました。

1916年1月に、東部戦線(eastern front)に兵士として駐留していたドイツの物理学者、カール・シュヴァルツシルト(Karl Schwarzschild)氏は、生後2ヶ月の重力理論となる、アルバート・アインシュタイン(Albert Einstein)の革命的な一般相対性理論(general relativity)の方程の最初の厳密解を生み出しました。一般相対性理論は重力をこう描きました、長い間理解されていた引力としてではなく、むしろ湾曲した空間と時間の影響としてです。シュヴァルツシルト解は、物質の静止した球の周囲での、時空の湾曲を明らかにしました。

奇妙なことに、シュワルツシルト氏はこれに気付きました、もしもこの物質が十分に小さい半径内に閉じ込められた(confined)のならば、中心に無限の曲率と密度の点－「シンギュラリティ(singularity)[特異点]」－があることに気づきました。

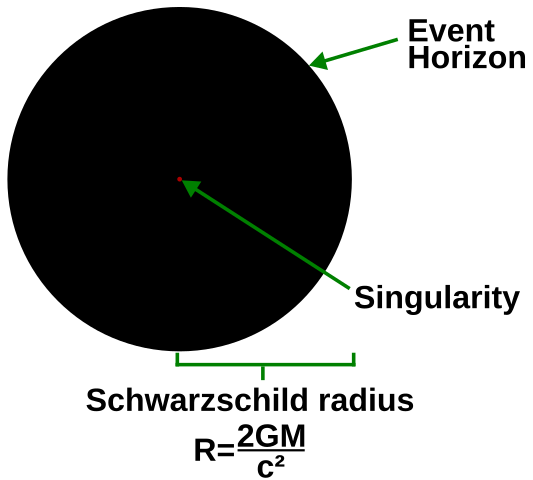
(追加図 Black hole details ウィキメディア経由CC4.0 クレジットSandstorm de)

物理学で無限が突然現れる(cropping up)ことは普通、警告の原因になります、そして兵士[戦った研究者]の結果を知ったアインシュタイン氏も、シュヴァルツシルト氏自身も、そのような天体が実際に存在するとは考えていませんでした。しかし、1970年代以降、この証拠は積み重なりました、宇宙にはこれらの実体がぞろぞろ(droves)と含まれています－「ブラックホール(black holes)」と授けられたのは、何故ならば、それらの重力がとても強く、それらの中に入るものは何も、光でさえも出て来ません。ブラックホール内部のシンギュラリティの性質は、それ以来ミステリーのままです。

最近、ハーバード大学(Harvard University)のブラックホール・イニシアチブ(Black Hole Initiative、BHI)と提携している研究者達のチームは、このパズルに関して大きく進歩させました。ポール・チェスラー(Paul Chesler)氏、ラメシュ・ナラヤン(Ramesh Narayan)氏、エリック・クリエル(Erik Curiel)氏は、天文学者達により研究されたものに似た、理論的なブラックホールの内部を調査し、どのような種類の特異点が内部に発見されるかを決定しようとしています。シンギュラリティは、量が本当に無限になる場所ではありませんが、しかし「一般相対性理論が破綻する場所」と、チェスラー氏は説明しました。そのような点で、一般相対性理論は、より正確な、未だ知られていない量子スケールの重力の記述に取って代わると考えられています。しかし、アインシュタインの理論が乱れる(haywire)ことが可能な、3つの異なる方法があり、3つの異なる種類の可能なシンギュラリティへつながります。「一般相対性理論がいつどこで破綻するのかを知ることは、それを超えた[量子重力の]理論は何か、を知るのに役に立ちます」と、チェスラー氏は述べました。

(d) What Happens if You Fall Into a Black Hole?　(2:18)　2015/06/11

BHIグループは、1963年に、数学者のロイ・カー(Roy Kerr)氏が、回転するブラックホールに対するアインシュタインの方程式を解いたとき、達成された大きな進歩に基づいて構築されました－実際には宇宙で全部が回転するので、シュヴァルツシルトが取った状況よりも、現実的な状況です。この問題はシュヴァルツシルトよりも困難でした、何故ならば、回転する天体は中央に外側への膨らみ(bulges)があり、それ故に球対称性(spherical symmetry)が欠けているからです。カー氏(e)の解は、回転するブラックホールの外側の領域を、明確に描写しましたが、しかし、内部は説明していませんでした。

(e) Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics | Physical Review Letters

カー氏のブラックホールは、依然としてやや非現実的でした、というのは物質を欠いた空間を占めていたからです。 BHIの研究者達が認識したこのことは、解を不安定にする効果がありました；単一の粒子の追加は、ブラックホールの内部の時空間の幾何学形状(geometry)を徹底的に変えるかもしれません。彼らのモデルをより現実的かつより安定させるための試みで、彼らは、彼らの理論的なブラックホールの中とその周囲に、「基本のスカラー場(elementary scalar field)」と呼ばれる特別な種類の物質を散在(sprinkled)させました。ところが、元のカー氏の解は、常に存在していた「永遠の」ブラックホールに関係するものでした。彼らの分析でのブラックホールは、宇宙でたくさんあるもののように重力崩壊から形成されました。

初めに、チェスラー氏、ナラヤン氏、クリエル氏は、このブラックホールに関して、彼らの方法論(methodology)をテストしました。これは、基本のスカラー場の中で物質の重力崩壊から形成された、帯電した非回転の球状ブラックホールです。彼らは、2月に科学プレプリントサイトarxiv.orgに投稿された論文(f)で、彼らの調査結果を詳しく説明しました。次に、チェスラー氏は、同様に形成された回転するブラックホールに関連した、より複雑な方程式に取り組みました、彼の単独の結果は3か月後に報告(g)されました。

(f) Singularities in Reissner-Nordström black holes | Arxiv
(g) Singularities in rotating black holes coupled to a massless scalar field | Arxiv

彼らの分析はこれを示しました、両方のタイプのブラックホールには、2つの異なる種類のシンギュラリティが含まれています。ブラックホールは、事象の地平線(event horizon)[事象の地平面]と呼ばれる球の中に入れられています：ひとたび物質や光がこの目に見えない境界を越えてブラックホールに入ると、脱出することはできません。事象の地平線の内側で、帯電した静止および回転するブラックホールは、内側の地平線(inner horizon)と呼ばれている戻ることのない第2の球面を持つことが知られています。チェスラー氏と彼の同僚達は、彼らが研究したブラックホールに対してこれを発見しました、「ヌル(null)」シンギュラリティが必然的に内側の地平線で形成されます、以前の結果と一致する発見です。ブラックホールの寿命のほとんどの間、物質と放射線はこの種のシンギュラリティを通過できます、とチェスラー氏は説明しましたが、しかし時が経つにつれて時空の曲率が指数関数的に増加し、「無限に遅い時間で、[時空の曲率が]無限になります。」

回転するブラックホールの内部の、空間的なシンギュラリティの発生に対して、このような直接的な導出が行われたのは、これが初めてです。
アモス・オリ(Amos Ori)

物理学者達は、彼らの準現実的なブラックホールが中心的なシンギュラリティを持つかどうかを、最も知りたかった－それは、単純なシュヴァルツシルトのブラックホールのために、確実に確立されただけだった事実です。そして、もしも中心的なシンギュラリティがあるのならば、彼らはそれが「空間的」かまたは「時間的」なのかを決定したかったのです。これらの用語は次の事実に由来しています。ひとたび粒子が空間的なシンギュラリティに近づくと、一般相対性理論の方程式を、時間的に進む方向に発展させることは不可能です；発展は空間方向にのみ許可されています。逆に、時間的なシンギュラリティに近づく粒子は、容赦なく内側に引き込まれません；それはまだ可能性のある未来を持っており、故に、時間を先に進めることができます、とはいえ空間内での位置は固定されています。外部の観測者達は、空間的なシンギュラリティを見ることができません、何故ならば、光波(light waves)は常にそれらへ動き、:決して出てくることがないからです。しかしながら、光波は時間的なシンギュラリティから出てくることができて、このことが外部の人に見えるようにします。

これら2つのタイプのうち、空間的なシンギュラリティは物理学者達より好ましいのかもしれません、何故ならば、一般相対性理論は、シンギュラリティ自体の点で破綻するだけだからです。時間的なシンギュラリティについて、理論はその点の周囲の至る所でつまづいています。例えば、物理学者は、放射線が時間的なシンギュラリティから現れるかどうか、そしてその強度(intensity)または振幅(amplitude)が何なのかもしれないことを、予測する方法がありません。

グループはこれを発見しました、彼らが調査したブラックホールの両方のタイプについて、確かに中心的なシンギュラリティがあり、それは常に空間的です。それは、意見を持っている天文学者達の大部分ではないにしても、多くの人がそうであると仮定されていましたと、チェスラー氏は述べました、「しかし、確かにそれは知られていませんでした。」

イスラエル(Israel)のハイファ(Haifa)にあるテクニオン(Technion)のブラックホール専門家である物理学者アモス・オリ(Amos Ori)氏は、チェスラー氏の新しい論文についてこう述べました、「私の知る限りでは、回転するブラックホールの内部での、空間的なシンギュラリティの発生に対して、このような直接的な導出が行われたのは、これが初めてです。」

ダートマス(Dartmouth)のマサチューセッツ大学(University of Massachusetts)の物理学者で、またブラックホールのシンギュラリティも調査しているガウラブ・カナ(Gaurav Khanna)氏は、BHIチームの研究をこう呼び出しました、「大きな進歩－この分野でのこれまでの努力を遙かに超える飛躍です。」

チェスラー氏と彼の協力者達はこのケースを強化しました、天体物理のブラックホールのそれらの中心核には空間的なシンギュラリティがあります。彼らは、未だそれを証明していません。彼らの次のステップは、基本的なスカラー場を超えてより現実的な計算を行うことで、そして、物質と放射線のより厄介なフォームを組み入れます。

チェスラーはこう強調しました、ブラックホールの計算に現れるシンギュラリティは、物理学者達が、それらの点で発見された極端な条件を処理できる重力の量子論(quantum theory)を作るときに、消えるはずです。チェスラー氏によれば、アインシュタインの理論を限界まで押し、それがどのように失敗するのかを正確に見る行為は、「次の理論を構築する上で、あなたを導くことができます」。

----- 出典 -----

Black Hole Singularities Are as Inescapable as Expected | Quanta Magazine

Singularities and Black Holes | Stanford Encyclopedia of Philosophy

Black Hole Singularities Are as Inescapable as Expected | NAUTILUS

Black Hole Singularities Are as Inescapable as Expected | SCRIBD

Black Hole Singularities Are as Inescapable as Expected | LaptrinhX

----- 2019/12/02公開の記事を読んで -----

アインシュタインの一般相対性理論をモデル化し、ミステリーとなっているシンギュラリティを理解しようとする試行錯誤です。

数学的な意味での特異点と、実際には物質が集中し詰まったブラックホールという天体の物理学的なニュアンスを区別するためにシンギュラリティという言葉にしています。

とにかく、シュワルツシルト解の言っていることは、その内側にあるブラックホールはどうやっても観測できません。なので、理論物理学の方法を使って、あーだこーだ想像しかできません。

一般的な天体同様にブラックホールが自転すると、シュワルツシルト半径も遠心力で変形するでしょう。実際、どの程度の自転速度なのでしょう。

Black hole - Wikipedia ( ブラックホール - Wikipedia )